MatSQ Docs - Appendix 2023 (en)
About　 Objectives Advantages Inquiry
Getting Started　 To create an account To learn more about the service To learn more about the services Tech Blog Webinar Free User Training To top-up credit
Account　
Work　 Configuration of the Work page To use Module To connect module Module Menu and Convenience Function Job submit Credit estimation To start with template Options of the work page
Modules 　 Modeling Structure builder Molecule Builder Special Quasirandom Structure Simulation DFT (Quantum Espresso) General Reaction Path (NEB) Phonon High Throughput DFT (SIESTA) General Pseudopotential Files DFT (GAMESS) GAMESS GAMESS-IRC GAMESS-NEB GAMESS-BDE MD (LAMMPS) Cascade EOS Thermal Conductivity Dislocation Tensile Test Melting & Quenching Custom MD (ChemLAMMPS) Thermalization Tg/CTE Elastic properties Dielectric constant Solubility parameter Viscosity (EMD) Viscosity (NEMD) Phase Diagram Calphad Machine Learning CGCNN Analysis Common Energy Movie Compare Structure Curve Fitting Tools Quantum Espresso QE Analysis Charge Density Density of States Band Structure Optical Property SIESTA Charge Density Density of States Band Structure Optical Property GAMESS Atomic Analysis Surfaces Density of States Vibration Frequency UV/Vis LAMMPS Molecule Analysis Etc. Memo
Data　 Move to Data page To read raw data file Find string File Types and Description To Compare Files To download a file
Troubleshooting　 Status Message Crash message(QE) Crash message(LAMMPS) Crash message(GAMESS)
Appendix　 Tutorial video To prepare a calculation model Quantum Espresso To learn about QE input Functional List SIESTA To learn about SIESTA input GAMESS To learn about GAMESS input LAMMPS To learn about LAMMPS input How to cite Calphad Introduction of Calphad Thermodynamics Database User-Defined Exmaples Function Diagram


MatSQ provides a tutorial video for users who are not familiar with the service.









How would you simulate materials used in your research with DFT? DFT can compute electronic structures for only a few to dozens of models because of the limitations of computing performance. Periodic boundary conditions were introduced as a way of overcoming these limitations and simulating a bulk condition similar to the macroscopic system. In periodic boundary conditions, a material is defined as follows:

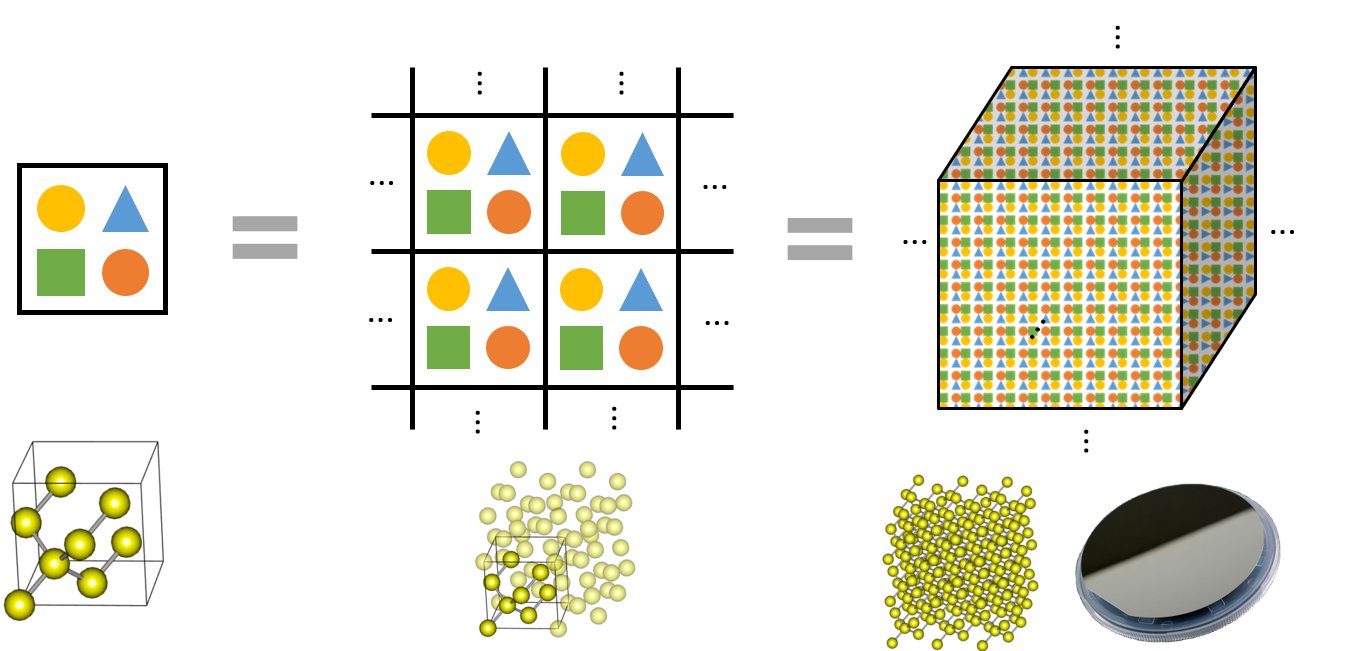
In periodic boundary conditions, a structure is repeated infinitely, so a silicon unit cell with eight atoms, a silicon supercell with 32 atoms, and a silicon bulk are theoretically identical. Moreover, because atoms are repeated by the space-group rules within the unit cell, silicon unit cells can be modeled only with the following information:


The computer recognizes a calculation model with a view that the structure shown on Structure Builder is repeated infinitely. If the cell size increases because of increased vacuum, the vacuum is recognized as repetitive, and the calculation is performed in the vacuum space too, so the amount of computation also increases. Roughly speaking, computational cost is proportional to V N (2 < N < 3), as the number of basis functions (plane waves) proportional to the volume of periodic unit cell. If you add a vacuum to model an atom, molecule, or slab structure, it is appropriate to have 10 to 15 Å clearance with the next repetitive model. You can check the repetitive structure by ticking "Ghost" in the right-click menu in the Visualizer Canvas of Structure Builder.


You can obtain the information or structure file required for unit cell modeling at the following link:





The following section gives a brief introduction to Quantum Espresso (QE), one of the DFT codes available on Materials Squire to run materials simulations. To understand in detail how Quantum Espresso works and what it can do, we recommend reading the documentation provided at www.quantum-espresso.org.


Quantum Espresso is an integrated suite of open-source computer codes for electronic-structure calculations and materials modeling at the nanoscale. It is based on the density-functional theory (DFT), plane waves, and pseudopotentials.
  • The Quantum Espresso package is an expandable distribution of related packages. Two core packages for DFT electronic structure calculations, PWscf (Plane Wave self-consistent field), and CP (Car-Parrinello Molecular Dynamics) are supplemented by various packages for specialized applications as well as plug-ins. For more information on all packages, refer to the Quantum Espresso official user guide .
  • Quantum Espresso provides open-source software packages. This means that everyone can study, expand, and modify the source code, allowing for continuous improvement.
  • The theory behind Quantum Espresso’s algorithm for electronic structure calculations and materials modeling is determined by the Kohn-Sham density functional theory (KS-DFT). In other words, the code implements the common iterative self-consistent method to solve the Kohn-Sham equations.
  • To perform materials simulations by a computer, we must expand functions like the wave function or the electron density in a basis set. Quantum Espresso uses plane waves as a basis set under the Bloch’s theorem. For the Gamma point, it is a Fourier series expansion of functions. A finite number of expansion coefficients, which is required for computation, can be achieved by an energy cutoff (ecutwfc, ecutrho).
  • Pseudopotentials are used to smoothen the Coulomb potential by atomic nucleis, resulting in fewer plane waves, without affecting the result too much. Quantum Espresso allows the use of various pseudopotentials (norm-conserving, ultrasoft, PAW). Choosing the pseudopotential for a given system is a science in itself. Refer to the Quantum Espresso documentation for further information.
Quantum Espresso is written mostly in Fortran-90. The code enables parallel computing.


Based on DFT, Quantum Espresso has numerous applications, ranging from ground-state energy calculations and structural optimization to molecular dynamics as well as the modeling of response and spectroscopic properties. DFT simulations can be done on any crystal structure or supercell, which features some form of periodicity. Furthermore, Quantum Espresso works for insulators, semiconductors, and metals, offering different options for k-point sampling as well as smearing of energy states. To speed up computations, Quantum Espresso can deal with various pseudopotentials and approximate exchange-correlation functionals. For more information, visit the Quantum Espresso website .


The Quantum Espresso input script contains all information about the system of interest and defines the calculation process. The information consists of the namelist and input_cards. The following figure shows the general syntax of the input script.

The Quantum Espresso code is a collection of input variables, which specify all information in a definitive format. Input variables can be real, integer, or character (string) values and must be entered in the syntax shown below. If an input parameter is not explicitly stated in the input script, it will be assigned with the default value. Refer to the Quantum Espresso pw.x description to see a complete set of input variables used in the PWscf (pw.x) calculations.


There are three mandatory namelists in the PWscf package:
  • It lists input variables that control the calculation process or determine the number of I/O. Examples include the calculation type, information amount (verbosity), and directory.
  • It includes input variables that determine the calculation system such as the number of atoms, Bravais lattice index, cutoff energies, and smearing methods.
  • It controls the algorithms used to reach the self-consistent solution of Kohn-Sham equations. Examples include the convergence threshold for self-consistency and mixing beta.
In addition to the above mandatory namelists, some calculations require the following namelists:
  • If the nuclei of the system are allowed to move in a calculation, this namelist contains necessary variables to control their motion. Variable atomic positions occur in molecular dynamics or structural relaxation computations.
  • Similar to &IONS, this namelist must be included for calculations with variable cell dimensions.
Quantum Espresso reads namelists in a specific order, whereas keywords (variables, keywords, tags) in each namelist can be inserted in an arbitrary order. Unnecessary namelists, such as &CELL in an scf calculation, is ignored.


For some input data, such as atomic coordinates, it is inconvenient to write it in the namelist syntax. To make life easier, Quantum Espresso, therefore, features input_cards that allow you to enter data in a more practical format. There are three mandatory input_cards to be entered:
  • Lists the name, mass, and PP of the atomic species included in a calculation model
  • Lists the name and coordinates of all atoms in a calculation model
  • Refers to the k-point grid and shift information, which are used to determine the number of k-points to be sampled in each lattice direction
CELL_PARAMETERS and OCCUPATIONS input cards do not have a specific order, but the data in each input card must follow a specific format to be read correctly. The following figure displays an example of the input script used in a graphene unit cell model. For more information on the input_card, refer to the PWscf input description .


The following links might be helpful to learn more about Quantum Espresso:






Parameter Value Description
Calculation type scf It performs self-consistent field calculations without affecting the atoms’ position. Namelists &IONS and &CELL are ignored in calculations. An iterative solution process runs to calculate the total energy, forces, and stresses.
relax In a relax calculation, the atoms are allowed to move to find their minimum energy (structural optimization). Includes geometric optimization steps and iterative self-consistent field calculations.
vc-relax It optimizes the structure for the atom position and the cell. The cell shape (angles, lattice constants) may change to find the optimized structure. It also includes geometric optimization steps and iterative self-consistent field calculations.
(vc-)md It calculates molecular dynamics with DFT. (ab-initio MD, AIMD)
restart nscf It performs non-scf calculations. Using this scheme, you make a single step calculation with the superposition of atomic orbitals. In contrast with the scf calculation, unoccupied electron states are also considered. Therefore, an nscf calculation is an economical choice for calculations that require a large k-point sampling.
bands It calculates only the Kohn-Sham states for the given set of k-points.
Max scf steps It determines the maximum number of scf algorithm runs until convergence is reached (scf is fixed to 1 unconditionally).
Information amount low Default
high It adds detailed information about k-points or the character table to a job.stdout file.
Force threshold It is the convergence threshold for the force to an ionic minimization. Any force for all elements must be less than this value (3.8E-4 Ry/Bohr = 0.01 eV/Å ).
Time step It sets the time step for an MD simulation (atomic unit, 1 a.u. = 4.8378*10^-17 s).

Parameter Value Description
occupations smearing It performs Gaussian smearing of occupation numbers on the assumption that an electron would occupy up to a point slightly above the balance band (suitable for metals).
fixed It calculates without smearing on the assumption that the structure is an insulator.
tetrahedra The tetrahedron method (P.E. Bloechl, PRB 49, 16223 (1994)) is used, which is suitable for DOS calculations. It must use a Monkhorst’s pack (automatic) k-point.
Ecut(wfc) It is the kinetic energy cutoffs for wave functions.
Ecut(rho) It is the kinetic energy cutoffs for charge densities and potentials. The default value is "ecutrho = 4*ecutwfc". Norm-conserving potentials and ultrasoft pseudopotentials require a higher ecut (rho) (about 8 to 12 times ecutwfc).
Gaussian broadeing It is the value required for Gaussian spreading in the Brillouin zone (broadening similar to '0.002 Ry = 27E-3eV = approx.300 K').
Number of electron spin 1 (all up) It calculates without considering the spin.
2 (up, down) It calculates taking into account the spin polarization. The amount of calculation doubles the case of "nspin=1."
4 (Noncolinear) It is used in noncollinear cases.
Van der Walls correction It is used to compensate data for models that are significantly affected by the Van der Waals force, such as a layered structure.
grimme-d2 (DFT-D) It corrects by the semi-empirical Grimme’s DFT-D2 method (S. Grimme, J. Comp. Chem. 27, 1787 (2006), V. Barone et al., J. Comp. Chem. 30, 934 (2009)).
grimme-d3 (DFT-D3) It corrects by the semi-empirical Grimme’s DFT-D3 method (S. Grimme et al., J. Chem. Phys 132, 154104 (2010)).
tkatchenko-scheffler It corrects the Tkatchenko-Scheffler dispersion with the C6 coefficient induced by the first principles (A. Tkatchenko and M. Scheffler, PRL 102, 073005 (2009)).
XDM It performs corrections with the exchange-hole dipole-moment model (A. D. Becke et al., J. Chem. Phys. 127, 154108 (2007), A. Otero de la Roza et al., J. Chem. Phys. 136, 174109 (2012)).
Hubbard_U the U parameter for the element of interest.

Parameter Value Description
Max iteration step Within an scf step, it sets the maximum step value for iteration, which continues until the convergence is completed. It is recommended to increase this value for structures with poor convergence.
Mixing beta The rate at which the final electron density is mixed with the initial electron density under the scf algorithm. It is recommended to decrease this value for structures with poor convergence.
Convergence threshold The value that sets the convergence threshold, which is the limit of the energy difference before and after an scf step.
Mixing mode plain The Broyden charge density mixing method
TF It adds a simple Thomas-Fermi screening (applicable to highly consistent systems).
local-TF It screens TF depending on the local density (applicable to highly consistent systems).
Starting wavefunction atomic It starts wave function calculations from the superposition of atomic orbitals. Calculations are performed normally in most cases, but some fail occasionally.
atomic+random In addition to the superposition of atomic orbitals, it considers random wave functions.
random It starts a calculation with random wave functions. It has a slower but safer start of scf.

Parameter Value Description
Ion dynamics It specifies the algorithm in Structural Relaxation to consider atomic movement.
relax bfgs It uses the BFGS quasi-newton algorithm for structural relaxation; cell_dynamics must be "bfgs" too. (Default).
damp It uses damped (quick-min Verlet) dynamics for structural relaxation.
vc-relax bfgs It uses BFGS quasi-newton algorithm; cell_dynamics must be "bfgs" too.
damp It uses damped (Beeman) dynamics for structural relaxation
md verlet It uses the Verlet algorithm to integrate Newton’s equation (Default).
langevin The ion dynamics is the overdamped Langevin.
langevin-smc The overdamped Langevin with Smart Monte Carlo (R.J. Rossky, JCP, 69, 4628 (1978)).
vc-md beeman It uses Beeman’s algorithm to integrate Newton’s equations (Default).
upscale It reduces conv_thr by conv_thr/upscale during structural optimization to increase accuracy when the relaxation approaches convergence (available in the bfgs option only).
Ion temperature (vc-)md not_controlled It does not control ionic temperatures (Default).
rescaling It controls ionic temperatures via velocity rescaling (first method).
md rescale-v It controls ionic temperatures via velocity rescaling (second method).
rescale-T It controls ionic temperatures via velocity rescaling (third method).
reduce-T It reduces ionic temperatures for every nraise step by the ΔT value.
berendsen It controls ionic temperatures with "soft" velocity rescaling.
andersen It controls ionic temperatures with the Andersen thermostat method.
initial It initializes ion temperatures to the starting temperature and leaves uncontrolled further on.
Starting temperature (K) The starting temperature in MD simulations.
ΔT Ion temperature = "rescale-T": At each step, the instantaneous temperature is multiplied by ΔT.
Ion temperature = "reduce-T": In every "nraise" step, the instantaneous temperature is reduced by ΔT.
nraise It rescales the instantaneous temperature (https://www.quantum-espresso.org/Doc/INPUT_PW.html#idm938).

Parameter Value Description
Cell dynamics It specifies the type of algorithms for variable cell relaxations to control the cell size.
bfgs The BFGS quasi-newton algorithm; ion_dynamics must be "bfgs" too.
none no dynamics
sd It is the steepest descent (not implemented).
damp-pr It is the damped (Beeman) dynamics of the Parrinello-Rahman extended lagrangian.
damp-w It is the damped (Beeman) dynamics of the new Wentzcovitch extended lagrangian.
Cell factor It is the maximum strain ratio of the cell size.
Press threshold It is the convergence threshold of the pressure applied to cells (Kbar).

Parameter Value Description
Sampling automatic It is an option to sample k-points in the Monkhorst-Pack method. It also distributes the k-point grid evenly to the supercell.
GAMMA It is similar to automatic 1x1x1 in that only one k-point is sampled, but there is a difference: the k-point is recognized as real rather than a complex number. It has the benefit of fast calculation.
crystal(_b) It designates the k-point as the relative coordinates to the reciprocal lattice vector. If the last column of data is {crystal}, it represents the weight for each k-point. If the last column of data is {crystal_b}, it represents the k-point number to be sampled by the next crystal coordination.
# k-points It is the number of k-points in the direction of the three lattice vectors, respectively.
shift It shifts the k-point grid with respect to the origin. Depending on the symmetry of the supercell, shifting the k-points could lead to better results.
crystal(_b) Path You can use a high-symmetric point to set the path for k-point sampling. You have to enter the weight.
weight crystal: the weight for each k-point to have
crystal_b: the number of k-points to be sampled until the next k-point




Option Description
ngauss Type of gaussian broadening
degauss Decide how much Gaussian Broadening will be done. You should note that the unit is Ry, not eV!
DeltaE Energy grid step (eV)
Emin Minimum of energy (eV) for DOS plot
Emax Maximum of energy (eV) for DOS plot

Option Description
spin_component Detemine the kind of spin when plotting the Band structure. In this time, the 'Spin-down' option can be selected when you performed the spin-polarized calculation.
lsym The bands will be classified according to the irreducible representation with considering the symmetry of k-points, if it set as '.TRUE.'.

Section Option Description
&INPUTPP Data to plot Detemine the data to obtain from the pp.x calculation. For further information, please refer to the link.
https://www.quantum-espresso.org/Doc/INPUT_PP.html#idm24
Planar/Macroscopic Average The number of points Set the density of datapoint of the result graph.
The size of the window Determine the number of the slab.

Section Option Value Description
&INPUTPP calculation eps Compute the complex macroscopic dielectric function, at the RPA (Random phase approximation) level, neglecting local field effects. eps is computed both on the real or imaginary axis.
jdos Compute the optical joint density of states.
&ENERGY_GRID Broadening Gaussian Apply the gaussian broadening.
Lorentzian Apply the Lorentzian broadening.
Inter-band Broadening (eV) Determine the broadening parameter
Intra-band Broadening (eV) Determine the broadening parameter
Frequency Range (eV) Determine the Frequency range
Frequency Mesh Set the number of datapoints
Optional Rigid Shift Give shift when calculating the transition energy.






This is the entire list of functions available in Quantum Espresso. Put 'Short name' in the DFT Functional input field.

Short nameComplete nameShort descriptionReferences
pzsla+pzPerdew-Zunger LDAJ.P.Perdew and A.Zunger, PRB 23, 5048 (1981)
bpb88+p86Becke-Perdew grad.corr.
pw91sla+pw+ggx+ggcPW91 (aka GGA)J.P.Perdew and Y. Wang, PRB 46, 6671 (1992)
blypsla+b88+lyp+blypBLYPC.Lee, W.Yang, R.G.Parr, PRB 37, 785 (1988)
pbesla+pw+pbx+pbcPBEJ.P.Perdew, K.Burke, M.Ernzerhof, PRL 77, 3865 (1996)
revpbesla+pw+rpb+pbcrevPBE (Zhang-Yang)Zhang and Yang, PRL 80, 890 (1998)
pw86pbesla+pw+pw86+pbcPW86 exchange + PBE correlation
b86bpbesla+pw+b86b+pbcB86b exchange + PBE correlation
pbesolsla+pw+psx+pscPBEsolJ.P. Perdew et al., PRL 100, 136406 (2008)
q2dsla+pw+q2dx+q2dcPBEQ2DL. Chiodo et al., PRL 108, 126402 (2012)
hcthnox+noc+hcth+hcthHCTH/120Handy et al, JCP 109, 6264 (1998)
olypnox+lyp+optx+blypOLYPHandy et al, JCP 116, 5411 (2002)
wcsla+pw+wcx+pbcWu-CohenZ. Wu and R. E. Cohen, PRB 73, 235116 (2006)
soggasla+pw+sox+pbecSOGGAY. Zhao and D. G. Truhlar, JCP 128, 184109 (2008)
optbk88sla+pw+obk8+p86 optB88
optb86bsla+pw+ob86+p86 optB86
ev93sla+pw+evx+nogcEngel-VoskoEngel-Vosko, Phys. Rev. B 47, 13164 (1993)
tpsssla+pw+tpss+tpssTPSS Meta-GGAJ.Tao, J.P.Perdew, V.N.Staroverov, G.E. Scuseria, PRL 91, 146401 (2003)
m06lnox+noc+m6lx+m6lcM06L Meta-GGAY. Zhao and D. G. Truhlar, JCP 125, 194101 (2006)
tb09sla+pw+tb09+tb09TB09 Meta-GGAF Tran and P Blaha, Phys.Rev.Lett. 102, 226401 (2009)
pbe0pb0x+pw+pb0x+pbcPBE0J.P.Perdew, M. Ernzerhof, K.Burke, JCP 105, 9982 (1996)
b86bxpb0x+pw+b86x+pbcB86bPBE hybrid
bhahlyppb0x+pw+b88x+blypBecke half-and-half LYP
hsesla+pw+hse+pbcHeyd-Scuseria-Ernzerhof (HSE 06, see note below)Heyd, Scuseria, Ernzerhof, J. Chem. Phys. 118, 8207 (2003); Heyd, Scuseria, Ernzerhof, J. Chem. Phys. 124, 219906 (2006).
b3lypb3lp+b3lp+b3lp+b3lpB3LYPP.J. Stephens,F.J. Devlin,C.F. Chabalowski,M.J. Frisch, J.Phys.Chem 98, 11623 (1994)
b3lypv1rb3lp+b3lpv1r+b3lp+b3lpB3LYP-VWN1-RPA
x3lypx3lp+x3lp+x3lp+x3lpX3LYPX. Xu, W.A Goddard III, PNAS 101, 2673 (2004)
vwn-rpasla+vwn-rpaVWN LDA using vwn1-rpa parametriz
gaupbesla+pw+gaup+pbcGau-PBE (also "gaup")
vdw-dfsla+pw+rpb +vdw1 vdW-DF1M. Dion et al., PRL 92, 246401 (2004); T. Thonhauser et al., PRL 115, 136402 (2015)
vdw-df2sla+pw+rw86+vdw2 vdW-DF2Lee et al., Phys. Rev. B 82, 081101 (2010)
vdw-df-c09sla+pw+c09x+vdw1 vdW-DF-C09
vdw-df2-c09sla+pw+c09x+vdw2 vdW-DF2-C09
vdw-df-obk8sla+pw+obk8+vdw1 vdW-DF-obk8 (optB88-vdW)Klimes et al, J. Phys. Cond. Matter, 22, 022201 (2010)
vdw-df-ob86sla+pw+ob86+vdw1 vdW-DF-ob86 (optB86b-vdW)Klimes et al, Phys. Rev. B, 83, 195131 (2011)
vdw-df2-b86rsla+pw+b86r+vdw2 vdW-DF2-B86R (rev-vdw-df2)
vdw-df-cxsla+pw+cx13+vdW1 vdW-DF-cxK. Berland and P. Hyldgaard, PRB 89, 035412 (2014)
vdw-df-cx0sla+pw+cx13+vdW1+HF/4 vdW-DF-cx-0K. Berland, Y. Jiao, J.-H. Lee, T. Rangel, J. B. Neaton and P. Hyldgaard, J. Chem. Phys. 146, 234106 (2017)
vdw-df2-0sla+pw+rw86+vdw2+HF/4 vdW-DF2-0
vdw-df2-br0sla+pw+b86r+vdW2+HF/4 vdW-DF2-b86r-0
vdw-df-c090sla+pw+c09x+vdw1+HF/4 vdW-DF-C09-0
vdw-df-xsla+pw+????+vdwx vdW-DF-x, reserved Thonhauser, not implemented
vdw-df-ysla+pw+????+vdwy vdW-DF-y, reserved Thonhauser, not implemented
vdw-df-zsla+pw+????+vdwz vdW-DF-z, reserved Thonhauser, not implemented
rvv10sla+pw+rw86+pbc+vv10rVV10R. Sabatini et al. Phys. Rev. B 87, 041108(R) (2013)





This is a brief introduction to SIESTA, a first-principles calculation code that can be used in Materials Square to perform material simulations. To understand more about how SIESTA works and what it can do, see https://siesta-project.org/siesta/.
SIESTA is a program that can perform electronic structure calculations and molecular dynamics simulations of molecules and solids. SIESTA versions 4.0 and later are released under the terms of the GPL open source license.

SIESTA is the same DFT-based calculation module as the "Quantum Espresso", but there are two major differences.
  • Unlike Quantum Espresso, which uses only Plan-Wave (PW), SIESTA uses plane waves and atomic basis functions (Basis set) to express electronic states. The electronic wave function is represented as a linear combination of atomic orbitals (LCAO), and the combined basis function use a plane wave to represent the entire space.
  • SIESTA calculation using the supercell technique (a method of calculating a large system by dividing it into small cells), allows for larger-scale system calculations than Quantum Espresso.






Parameter Value Description Note
Calculation Type
default = SCF 		Select the overall calculation type.
SCF Perform electronic structure calculations with fixed cell sizes and atom positions.
Relax Perform calculations to optimize the structure by fixing the cell size and moving the positions of the atoms.
VC-relax Perform calculations to optimize the structure by changing the cell size and moving the positions of the atoms.
Phonon Perform the phonon calculations which are calculations of vibration modes between atoms.
MD Perform the Ab-Initio molecular dynamics (AIMD).
MD Type
default = NVE 		Select the desired MD calculation type. Enabled when Calculation Type=MD is selected.
NVE (Verlet) Perform AIMD simulation with standard Verlet algorithm.
NVT (Nose) Perform AIMD simulation with temperature controlled by the Nosé thermostat algorithm.
NPE (PR) Perform AIMD simulation with pressure controlled by the Parrinello-Rahman method.
NPT (Nose-PR) Perform the AIMD with temperature controlled by means of a Nosé thermostat and pressure controlled by the Parrinello-Rahman method.
Anneal-Temp. MD with annealing to a desired temperature. Reach a target temperature by velocity rescaling.
Anneal-Pressure MD with annealing to a desired pressure. Reach a target pressure by scaling of the unit cell size and shape.
Anneal-Temp. & Pressure MD with annealing to a desired temperature and pressure. Reach a target temperature and pressure by velocity rescaling and by scaling of the unit cell size and shape.
Max. optimization steps
default = 500 		Set the maximum number of steps in a structural optimization cycle. If the "Force Tolerance" value is reached before the maximum number of steps is reached, the structural optimization calculation will stop. Enabled when Calculation Type=VC-relax or relax is selected.
Force Tolerance (eV/Ang)
default = 0.001 		Set the force tolerance for structure optimization. If the maximum atomic force is less than this value, the calculation will stop. Enabled when Calculation Type=VC-relax or relax is selected.
Stress Tolerance (GPa)
default = 0.01 		Set the stress tolerance value for the cell size optimization calculation (vc-relax). If the maximum atomic force is smaller than "Force Tolerance" and the maximum stress component is smaller than "Stress Tolerance", the calculation will stop. Enabled when Calculation Type = VC-relax is selected.
External E Field
default = OFF 		Specify an external electric field for the calculation. This option is performed only in calculations for molecules, chains, or slabs. The direction of the electric field must be set to be perpendicular to the bulk direction. (It is not possible to set the electric field for bulk structures such as dielectrics or ferroelectrics.)
Dipole Correction
default = OFF 		This option causes the electric field required to compensate the dipoles of the system to be calculated at each iteration of the self-consistent cycle. This option is not available on a charged system (Netcharge $(\neq)$ 0).
The dipole of the system is calculated via
$(D = -e\int(r-r_{0})\delta\rho(r))$
where $(r_{0})$ is the dipole origin, and $(\delta\rho(r))$ is valence pseudocharge density minus the atomic valence pseudocharge densities.
Supercell Size
default = 1,1,1 		This creates a supercell by extending it by $(\pm n)$ in each direction for phonon calculation supercell. For example, if you set the x, y, and z values to 2,2,1, the total cell size will be 5$(\times)$5$(\times)$1. Enabled when calculation Type=Phonon is selected.
Displacement (Bohr)
default = 0.04 		Set the displacement to use for the computation of the force constant matrix for phonon calculations. Enabled when calculation Type=Phonon is selected.

Parameter Value Description Note
Functional type
default = GGA 		Select the exchange-correlation functional type to use for simulation.
LDA Perform a Local Density Approximation (LDA) calculation. Potential File must be set to LDA type.
GGA Perform a Generalized Gradient Approximation (GGA) calculation. Potential File must be set to GGA type.
VDW Perform a van der Waals (VDW) calculation. The Potential File must be set up by the user.
Authors
default = PBE 		Particular parametrization of the exchange-correlation functional.
CA (= PZ): (Spin) local density approximation (LDA/LSD).
Quantum Monte Carlo calculation of the homogeneous electron gas by D. M. Ceperley and B. J. Alder, Phys. Rev. Lett. 45,566 (1980), as parametrized by J. P. Perdew and A. Zunger, Phys. Rev B 23, 5075 (1981) 		Enabled when Functional Type=LDA is selected.
PW92 LDA/LSD, as parametrized by J. P. Perdew and Y. Wang, Phys. Rev B 45, 13244 (1992) Enabled when Functional Type=LDA is selected.
PW91 Generalized gradients approximation (GGA) of Perdew and Wang. Ref: P&W, J. Chem. Phys. 100, 1290 (1994) Enabled when Functional Type=GGA is selected.
PBE GGA of J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996) Enabled when Functional Type=GGA is selected.
revPBE Modified GGA-PBE functional of Y. Zhang and W. Yang, Phys. Rev. Lett. 80, 890 (1998) Enabled when Functional Type=GGA is selected.
RPBE Modified GGA-PBE functional of B. Hammer, L. B. Hansen and J. K. Norskov Phys. Rev. B 59, 7413 (1999) Enabled when Functional Type=GGA is selected.
PBEsol Modified GGA-PBE functional of J. P. Perdew et al, Phys. Rev. Lett. 100, 136406 (2008) Enabled when Functional Type=GGA is selected.
BLYP (=LYP) GGA with Becke exchange (A. D. Becke, Phys. Rev. A 38, 3098 (1988)) and Lee-Yang-Parr correlation (C. Lee, W. Yang, R. G. Parr, Phys. Rev. B 37, 785 (1988)), as modified by B. Miehlich, A. Savin, H. Stoll, and H. Preuss, Chem. Phys. Lett. 157, 200 (1989). Enabled when Functional Type=GGA is selected.
DRSLL (=DF1) van der Waals density functional (vdW-DF) of M. Dion, H. Rydberg, E. Schröder, D. C. Langreth, and B. I. Lundqvist, Phys. Rev. Lett. 92, 246401 (2004), with the efficient implementation of G. Román-Pérez and J. M. Soler, Phys. Rev. Lett. 103, 096102 (2009) Enabled when Functional Type=VDW is selected.
LMKLL (=DF2) vdW-DF functional of Dion et al (same as DRSLL) reparametrized by K. Lee, E. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B 82, 081101 (2010) Enabled when Functional Type=VDW is selected.
KBM dW-DF functional of Dion et al (same as DRSLL) with exchange modified by J. Klimes, D. R. Bowler, and A. Michaelides, J. Phys.: Condens. Matter 22, 022201 (2010) (optB88-vdW version) Enabled when Functional Type=VDW is selected.
BH vdW-DF functional of Dion et al (same as DRSLL) with exchange modified by K. Berland and P. Hyldgaard, Phys. Rev. B 89, 035412 (2014) Enabled when Functional Type=VDW is selected.
VV vdW-DF functional of O. A. Vydrov and T. Van Voorhis, J. Chem. Phys. 133, 244103 (2010) Enabled when Functional Type=VDW is selected.
Basis Size
default = DZP 		Select the basis set to use for simulation.
SZ Use single zeta basis.
DZ Use double zeta basis.
SZP Use single zeta basis plus polarization orbitals.
DZP Use double zeta basis plus polarization orbitals.
Energy Shift (Ry)
default = 0.02 		Set the standard for orbital-confining radii of the first-zeta PAO.
Spin-polarization
default = non-polarized 		Select the spin component of the simulation.
non-polarized Perform a calculation with spin-degeneracy (only one component).
polarized Perform a calculation with colinear spin (two spin components).
non-collinear Perform a calculation with non-colinear spin (4 spin components), up-down and angles. This calculation requires you entering the spin component in manual mode.
spin-orbit Perform a calculation with spin-orbit coupling. This requires the pseudopotentials to be relativistic. Relativistic pseudopotentials must be used.
Net Charge (e)
default = 0 		Specify the net charge of the system. For example, the $(F^{-})$ ion would have NetCharge -1 , and the $(Na^{+})$ ion would have NetCharge 1.
Spin Fix
default = False 		Choose whether to fix the spin value of the system. Enabled when Spin-polarization=polarized is selected.
Total Spin
default = 0 		Define the value of the imposed total spin polarization of the system (in units of the electron spin, 1/2). Enabled when Spin Fix=True is selected.
Spin Option
default = False 		Define the initial spin density for a spin polarized calculation atom by atom. The desired initial spin-polarization (real, positive for spin up, negative for spin down).

Parameter Description Note
SCF Must Converge
default = TRUE 		This option stops the calculation if convergence is not achieved even after proceeding with the specified maximum number of SCF iterations.
Mesh Cutoff (Ry)
default = 300 		Define the plane wave cutoff for the grid.
Max. SCF Iterations
default = 1000 		Define the maximum number of SCF iterations.
SCF DM Tolerance
default = 0.00001 		Define the tolerance of the Density Matrix. The SCF calculation will be considered complete when the maximum difference between the output and input of each element of the DM during an SCF cycle is smaller than SCF.DM.Tolerance.
Mixing Weight
default = 0.1 		Define the mixing ratio of the electron density obtained in the previous step and the initial electron density in SCF cycle.
Mixing History
default = 6 		Specify the number of previous SCF steps used to estimate the inputs used in the next SCF calculation.
Electronic Temperature (K)
default = 300 		Specify the temperature of the Fermi-Dirac or Methfessel-Paxton distribution. It is particularly useful when calculating metallic systems, and in some cases to speed up the convergence of SCF calculations.

Parameter Description Note
Grid Set the k-point sampling using Monkhorst's Pack method. Divide the reciprocal lattice space (Brillouin zone) into equal intervals as much as the set grid and sample the k-points corresponding to the lattice points.
Shift
default = OFF 		This is an option to move the k-point grid based on the origin. (off: 0.0 0.0 0.0; on: 0.5 0.5 0.5)

Parameter Description Note
Length Time Step (fs)
default = 1 		Set the length of the time step of the AIMD simulation.
MD Step
default = 100 		Set the final time step of the MD simulation. The final time of the AIMD will be Length Time Step*MD step.
Initial Temp. (K)
default = 300 		Specifies the initial temperature for the AIMD simulation. Atoms are assigned random rates from the Maxwell-Boltzmann distribution along with their corresponding temperatures.
Target Temp. (K)
default = 300 		Specifies the target temperature in the AIMD simulation. It is used in NVT, NPT using Nose thermostat or annealing calculations among MD types. Enabled when MD Type=NVT, NPT, Anneal-Temp., or Anneal-Temp.&Pressure is selected.
Target Pressure (GPa)
default = 1 		Specifies the target pressure in the AIMD simulation. Useful for cell optimizations and constant-pressure molecular dynamics. Enabled when Calculation Type=vc-relax or MD Type=NPE, NPT, Anneal-Pressure, or Anneal-Temp.&Pressure is selected.
Generalized Mass (Ry fs2)
default = 100 		Specifies the generalized mass of the Nose or Parrinello-Rahman variable. This determines the time scale of the Nose or Parrinello-Rahman variable dynamics, and its coupling to the physical system. If MD Type=NVT, MD.NoseMass is specified, If MD Type=NPE, MD.ParrinelloRahmanMass is assigned.
Relaxation Time (fs)
default = 100 		Specifies the relaxation time to reach target temperature and/or pressure in annealing MD. Note that this is a "Relaxation Time", and as such it gives a rough estimate of the time needed to achieve the given targets. Enable when MD Type=Anneal-Temp., Anneal-Pressure, or Anneal-Temp.&Pressure is selected.
Estimate of Bulk Modulus (Ry/Bohr3)
default = 100 		Specifies an estimate (may be rough) of the bulk modulus of the system. This is needed to set the rate of change of cell shape to reach target pressure in annealing MD. Enable when MD Type=Anneal-Pressure, or Anneal-Temp.&Pressure is selected.





Parameter Value Description Note
Charge Density (3D) Post-processing option to view Charge Density and Potential as a 3D structures.
Total Charge Density Total charge density, up/down spin charge density, and spin difference density are extracted as 3D structure files.
Local Charge Density Local charge density, up/down spin charge density, and spin difference density are extracted as 3D structure files. Only enable when LDOS post-processing is connected to a completed calculation.
Total Electrostatic Potential Electrostatic potential is extracted as 3D structure files.
Total Potential Total potential is extracted as 3D structure files.
Macroscopic/Planar average (2D) Post-processing option to view Charge Density and Potential as a 2D structures.
MWhen calculating macroscopic average (nanosmoothing), the data is output at the value set by the user. The set values are written to the macroave.in file.
Charge Density The macroscopic average and planar average of charge density are extracted as 2D graph.
Electrostatic Potential The macroscopic average and planar average of electrostatic potential are extracted as 2D graph.
# of convolutions
default=1 		Select the number of square filter functions in the macroaverage (nanosmoothing). (1 = surfaces, 2= Interfaces and superlattices)
Length of the first step function (bohr)
default=2.96687 		First length for the filter function in macroscopic average.
Length of the second step function (bohr)
default=2.96687 		Second length for the filter function in macroscopic average This setting is only affected when # of convolutions=2.
Total number of electrons
default=501 		Sets the total number of electrons in the system. This value is only used for renormalization when calculating the macroscopic average (nanosmoothed ). This setting is only affected when checking Charge Density as a 2D structure.

Parameter Description Note
Minimum Energy (eV)
default = -20 		Set the minimum of the energy range for PDOS.
Maximum Energy (eV)
default = 10 		Set the maximum of the energy range for PDOS.
Broadening (eV)
default = 0.1 		Set the peak width (an energy) for broadening the eigenvalues.
K-point Set the interval to sample k-points with the same Monkhorst's Pack method as the general calculation and choose whether to shift the grid or not.
For accurate analysis, it is recommended to increase it by about 2~3 times than in the General calculations such as vc-relax, relax, or SCF.

Parameter Description Note
Minimum Energy (eV)
default = -0.5 		Set the minimum of the energy range for LDOS.
Maximum Energy (eV)
default = 0 		Set the maximum of the energy range for LDOS.

Parameter Description Note
Crystal System
default = Cube 		Select the crystal system from which to sample the high-symmetric point. It is recommended to set it to the same crystal system as the calculation model used.
Number of k-points
default = 10 		Specifies the number of gaps between each k-point in the grid vector direction.
High symmetry points You can set the K-point path directly. High symmetry points are added by clicking on each K-point. Default is set to the path of the crystal selected in the Crystal system.
Band Lines Shows the set high-symmetric K-point path and number of intervals. You can also make your own edits here.

Parameter Value Description Note
Minimum Energy (eV)
default = 0 		Specifies the minimum of the energy range in which the frequency spectrum will be calculated.
Maximum Energy (eV)
default = 20 		Specifies the maximum of the energy range in which the frequency spectrum will be calculated.
Broadening (eV)
default = 0.5 		Specifies the Gaussian broadening to be applied to the frequency values.
Mesh point
default = 4, 4, 2 		Determine the mesh size used for the integration across the Brillouin zone.
Polarization Type
default = polycrystal 		Select the type of polarization to be used in the calculation.
polycrystal default
polarized The electric field is applied in the direction set in Optical Vector.
unpolarized Light propagates in the direction set in Optical Vector.
Optical Vector
default = 0, 0, 1 		Sets the vector direction for either the electric field (polarized) or light propagation (unpolarized). Enable when Polarization Type = polarized or unpolarized is selected






This is a brief introduction to GAMESS, the first-principle calculation code available in Material Square. For more information on how GAMESS works and possible applications, refer the official manual at https://www.msg.chem.iastate.edu/gamess/


GAMESS is a program for ab initio molecular quantum chemistry. Briefly, GAMESS can compute SCF wavefunctions ranging from RHF, ROHF, UHF, GVB, and MCSCF. Correlation corrections to these SCF wavefunctions include Configuration Interaction, second order perturbation Theory, and Coupled-Cluster approaches, as well as the Density Functional Theory approximation. Excited states can be computed by CI, EOM, or TD-DFT procedures. Nuclear gradients are available, for automatic geometry optimization, transition state searches, or reaction path following. Computation of the energy hessian permits prediction of vibrational frequencies, with IR or Raman intensities. Solvent effects may be modeled by the discrete Effective Fragment potentials, or continuum models such as the Polarizable Continuum Model. Numerous relativistic computations are available, including infinite order two component scalar relativity corrections, with various spin-orbit coupling options.

A variety of molecular properties, ranging from simple dipole moments to frequency dependent hyperpolarizabilities may be computed. Many basis sets are stored internally, together with effective core potentials or model core potentials, so that essentially the entire periodic table can be considered.

Most computations can be performed using direct techniques, or in parallel on appropriate hardware.





This group specifies the type of wavefunction, the type of calculation, use of core potentials, spherical harmonics, coordinate choices, and similar fundamental job options.

ParameterValueDescription
SCF Type RHF (Default)Restricted Hartree Fock calculation
UHFUnrestricted Hartree Fock calculation
ROHFRestricted open shell Hartree-Fock.
MCSCFMulticonfigurational SCF wavefunction
MPLEVL Chooses Møller-Plesset perturbation theory level, after the SCF. See $MP2, or $MRMP for MCSCF.
0 (Default)Skip the MP computation
2Perform second order energy correction.
RUN Type ENERGY (Default)Molecular energy without structure optimization
HESSIANMolecular energy plus gradient plus second derivatives, including harmonic vibrational analysis. See the $FORCE and $CPHF input groups.
OPTIMIZEOptimize the molecular geometry using analytic energy gradients. See $STATPT.
SADPOINTLocate saddle point (transition state). See $STATPT.
RAMANcomputes Raman intensities, see $RAMAN.
DFT Type NONE (Default)ab initio computation (Hartree-Fock Method)
BLYPperform density functional theory run, using the functional specified. Please refer to the following link to look at the 'DFTTYP' tag description. https://www.msg.chem.iastate.edu/gamess/GAMESS_Manual/docs-input.txt
B3LYP
PBE
PBE0
PW91
REVPBE
TDDFT NONE (Default)no excited states
EXCITEgenerate time-dependent DFT excitation energies, using the DFTTYP= functional, for RHF or UHF references. Analytic nuclear gradients are available for RHF. See $TDDFT.
Charge Total charge of the molecular system
0 (Default)Neutral
+1, -1, -2, ...monovalent cation, monovalent anion, divalent anion, ...
Multiplicity Multiplicity of the electronic state
1 (Default)Singlet
2, 3, …doublet, triplet, and so on.
ISPHER Spherical Harmonics option
-1 (Default)Use Cartesian basis functions to construct symmetry-adapted linear combination (SALC) of basis functions. The SALC space is the linear variation space used.
0Use spherical harmonic functions to create SALC functions, which are then expressed in terms of Cartesian functions. The contaminants are not dropped, hence this option has EXACTLY the same variational space as ISPHER=-1. The only benefit to obtain from this is a population analysis in terms of pure s,p,d,f,g functions.
1Same as ISPHER=0, but the function space is truncated to eliminate all contaminant Cartesian functions [3S(D), 3P(F), 4S(G), and 3D(G)] before constructing the SALC functions. The computation corresponds to the use of a spherical harmonic basis.
PP NONE (Default)All electron calculation
SBKJCStevens/Basch/Krauss/Jasien/Cundari valence basis set, for Li-Rn. This choice implies an unscaled -31G basis for H-He.
HWHay/Wadt valence basis. This is a -21 split, available Na-Xe, except for the transition metals. This implies a 3-21G basis for H-Ne.
MCPSelect PP=MCP in $CONTRL to automatically use the model core potential matching your basis choice below. References for these bases, and other information about MCPs can be found in the REFS.DOC chapter. Another family covering almost all elements is available in $DATA only.
READRead ECP potentials in the $ECP input.


This group allows certain standard basis sets to be easily requested. Basis sets are specified by several keywords: GBASIS, NDFUNC, BASNAM, etc.

ParameterClassValueKeywordsDescriptionAvailable Elements
BASISSemiempiricalAM1GBASIS=AM1selects AM1 model HamiltonianC, H, O, N
PM3GBASIS=PM3selects PM3 model HamiltonianH, C-F, Al-Cl, Br, I
Gaussian functionsSTO-3GGBASIS=STO NGAUSS=3Pople's STO-NG minimal basis set.H-Xe
3-21G (Default)GBASIS=N21 NGAUSS=3Pople's N-21G split valence basis set + 3 gaussian functions.H-Xe
6-31G*GBASIS=N31 NGAUSS=6 NDFUNC=1Pople's N-31G split valence basis set + 6 gaussian functions and heavy atom polarization functions.H-Kr
6-311G**GBASIS=N311 NGAUSS=6 NDFUNC=1 NPFUNC=1Pople's "triple split" N-311G basis set + 6 gaussian functions, heavy atom polarization functions, and p type polarization functions for light atom (H-He).H-Ne
6-311G**+GBASIS=N311 NGAUSS=6 NDFUNC=1 NPFUNC=1 DIFFSP=.TRUE.Pople's "triple split" N-311G basis set + 6 gaussian functions, p type polarization functions for light atom (H-He), and polarizaiton function, diffuse function for heavy atoms.H-Ne
Auxiliary basis setcc-pVDZGBASIS=CCDcc-pVDZ basisH-Ar
cc-pVTZGBASIS=CCTcc-pVTZ basisH-Ar
aug-cc-pVDZGBASIS=ACCDaug-cc-pVDZ basisH-Ar
Effective Core Potential (ECP)SBKJCGBASIS=SBKJCStevens/Basch/Krauss/Jasien/Cundari valence basis set, for Li-Rn. This choice implies an unscaled -31G basis for H-He.H-Rn
Customdef2-svpGBASIS=d2svp EXTFIL=.TRUE.Custom basis set for heavy metal elementsH-Rn, La-Lu
def2-tzvpGBASIS=d2tzvp EXTFIL=.TRUE.Custom basis set for heavy metal elementsH-Rn, La-Lu
LANL2DZGBASIS=lanl2dz EXTFIL=.TRUE.Custom basis set for heavy metal elementsH-Bi, La, U-Pu
CUSTOMGBASIS={User Define} EXTFIL=.TRUE.Please refer to the following link to look at the 'GBASIS' tag description. https://www.msg.chem.iastate.edu/gamess/GAMESS_Manual/docs-input.txt

You can download your custom basis set from Basis Set Exchange.
https://www.basissetexchange.org/		User Define


This group controls the selection of initial molecular orbitals.

ParameterValueDescription
Initial Orbital Write type of initial orbital guess.
Huckel (Default) Carry out an extended Huckel calculation using a Huzinaga MINI basis set, and project this onto the current basis. This is implemented for atoms up to Rn, and will work for any all electron or core potential basis set. (default for most runs)
HCORE Diagonalize the one electron Hamiltonian to obtain the initial guess orbitals. This method is applicable to any basis set, but does not work as well as the HUCKEL guess.
MOREAD Read in formatted vectors punched by an earlier run. This requires a $VEC deck, and you MUST pay attention to NORB below.
RDMINI Read in a $VEC deck from a converged SCF calculation using GBASIS=MINI, to project the MINI orbitals onto the current basis. The option improves upon the Huckel guess because it involves SCF orbitals, which are typically easily obtained in the small MINI basis. This option doesn't work if the current basis uses core potentials. potentials. The $VEC from the MINI run must contain all virtual orbitals.
MOSAVED (default for restarts) The initial orbitals are read from the DICTNRY file of the earlier run.
SKIP Bypass initial orbital selection. The initial orbitals and density matrix are assumed to be in the DICTNRY file. Mostly used for RUNTYP=HESSIAN when the hessian is being read in from the input.


This group controls solvent effect computations using the Polarizable Continuum Model.
The default calculation, chosen by selecting only the SOLVNT keyword, is to compute the electrostatic free energy. Appropriate numerical constants are provided for a wide range of solvents.
Additional keywords (ICOMP, ICAV, IDISP, or IREP/IDP) allow for more sophisticated computations, namely cavitation, repulsion, and dispersion free energies. The methodology for these is general, but numerical constants are provided only for water.

ParameterValueDescription
Solvent effectNONE (Default)
WATERWater (H2O)
CH3OHMethanol (CH3OH)
C2H5OHEthanol (C2H5OH)
CLFORMChloroform (CHCl3)
CTCLCarbon Tetrachloride (CCl4)
METHYCLMethylene Chloride (CH2Cl2)
12DCLET1,2-Dichloroethane (CH2ClCH2Cl)
BENZENEBenzene (C6H6)
TOLUENEToluene (C6H5CH3)
CYClOHEXANECyclohexane (C6H12)
CUSTOMACETONEAcetone (CH3COCH3)
ANILINEAniline (C6H5NH2)
CLBENZChlorobenzene (C6H5Cl)
DMSODimethylsulfoxide (DMSO)
NEPTANEN-Heptane (C7H16)
NITMETNitromethane (CH3NO2)
THFTetrahydrofuran (THF)


This group controls the computation of the hessian matrix (the energy second derivative tensor, also known as the force constant matrix), and an optional harmonic vibrational analysis. This can be a very time consuming calculation. However, given the force constant matrix, the vibrational analysis for an isotopically substituted molecule is very cheap. Related input is HESS= in $STATPT, and the $MASS, $HESS, $GRAD, $DIPDR, $VIB inputs. Calculation of the hessian automatically yields the dipole derivative tensor, giving IR frequencies. Raman intensities are obtained by following with RUNTYP=RAMAN.

ParameterValueDescription
METHODchooses the computational method
ANALYTIC (Default)ANALYTIC is a fully analytic calculation. This is implemented for SCFTYP=RHF, UHF, ROHF, GVB (for NPAIR=0 or 1, only), and MCSCF (for CISTEP=ALDET or ORMAS, only). R-DFT and U-DFT are also analytic.
SEMINUMSEMINUM does numerical differentiation of analytically computed first derivatives. This is the default for UHF, MCSCF using other CISTEPs, all solvent models, relativistic corrections, and most MP2 or CI runs.
FULLNUMFULLNUM numerically differentiates the energy twice, which can be used by all other cases. It requires many energies (a check run will tell how many) and so it is mainly useful for systems with only very few symmetry unique atoms.
Temperature (K)298.15 (Default)An array of up to ten temperatures at which the thermochemistry should be printed out. The default is a single temperature, 298.15 K. To use absolute zero, input 0.001 degrees.


This group controls the search for stationary points (ground state).

ParameterValueDescription
Convergence tolerance (Hartree/Bohr) 0.0001 (Default)Gradient convergence tolerance (unit: Hartree/Bohr)
Convergence of a geometry search requires the largest component of the gradient to be less than OPTTOL, and the root mean square gradient less than 1/3 of OPTTOL.
Max iteration step 500 (Default)The maximum number of steps to take. Restart data is punched if NSTEP is exceeded. The default is 50 steps for a minimum search, but only 20 for a transition state search, which benefit from relatively frequent Hessian re-evaluations.
Hessian matrixGUESS (Default)GUESS chooses an initial guess for the hessian. (default for RUNTYP=OPTIMIZE)
CALCCompute the hessian, see $FORCE input.
IR frequencyFlag to control automatic hessian evaluation at the end of a successful geometry search. (default=.FALSE.)


This group generates molecular excitation energies by time-dependent density functional theory computations (or time-dependent Hartree-Fock, also known as the Random Phase Approximation).

Parameter Value Description
Nstate 10 (Default) Number of states to be found (excluding the reference state). The default is 1 more state.
MULT 1 (Default) Multiplicity (1 or 3) of the singly excited states. This keyword applies only when the reference is a closed shell. This parameter is ignored when TDDFT=SPNFLP.






This is a brief introduction to LAMMPS, the molecular dynamics code available in Material Square. For more information on how LAMMPS works and possible applications, refer the official manual at lammps.sandia.gov.


LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) is a classical molecular dynamics simulation code, developed at the Sandia National Laboratory, it designed to be calculated effectively with parallel computing. Base on Newton's equation of motion, LAMMPS can calculate a system consists of several hundred to several billion atoms using forcefield for fast speed. It can calculate not only the stability at the given temperature which is a basic property in the materials study, but also mechanical, thermal and chemical properties of material. Recently, the effectivity of parallel computing using the Graphics Processing Unit (GPU) was increased, and machine learning can be used for the expanding interatomic potential.




Parameter Value Description
Reactive Forcefield ID The identification value of each reactive forcefield
Type The type of reactive forcefield
Elements Elements for the reactive forcefield to consider
Author The author of the reactive forcefield
DOI The paper on the corresponding reactive forcefield
Ensemble NVT An NVT ensemble is also known as the canonical ensemble. It assumes a calculation model as an isolated system, which has a fixed temperature, volume, and the number of atoms.
NVE An NVE ensemble is also known as the microcanonical ensemble. This assumes a calculation model as an isolated system, which cannot exchange energy or particles with its environment because the energy of the system is fixed.
After Relax Before starting an MD simulation, a structural relaxation is performed at room temperature (200 K – 300 K) first for structural stabilization. It can reduce the probability that the calculation would fail because of structural instability.
Dump It saves the trajectory in a file for every step selected. For calculations with long simulation times, you can reduce the overall file size.
Temperature Begin (K) The temperature at the start of a simulation
Final (K) The target temperature during simulation
Damping (Step) Resets the temperature for each damping step
Time (ps) Specifies the total simulation time (1 ns = 1000 ps)
Initial Velocity (Å/fs) The initial speed of the atom group selected
Force (Kcal/mole-Å) The force per fs applied to the selected atom group
Move (Linear, Å/fs) The distance traveled per fs for the selected atom group




Please add citation by the URL to cite the Materials Square.
Please refer to Acknowledgement page to cite the simulation packages implemented in Materials Square.



First-principles calculations were performed using Quantum ESPRESSO [1],[2] package implemented in Materials Square [3].
[1] Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., ... & Wentzcovitch, R. M. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of physics: Condensed matter, 21(39), 395502.
[2] Giannozzi, P., Andreussi, O., Brumme, T., Bunau, O., Nardelli, M. B., Calandra, M., ... & Baroni, S. (2017). Advanced capabilities for materials modelling with Quantum ESPRESSO. Journal of physics: Condensed matter, 29(46), 465901.
[3] Virtual Lab. Inc., (2017, January 01). Materials Square. https://www.materialssquare.com/

First-principles calculations were performed using GAMESS [1] package implemented in Materials Square [2].
[1] Barca, G. M., Bertoni, C., Carrington, L., Datta, D., De Silva, N., Deustua, J. E., ... & Gordon, M. S. (2020). Recent developments in the general atomic and molecular electronic structure system. The Journal of chemical physics, 152(15), 154102.
[2] Virtual Lab. Inc., (2017, January 01). Materials Square. https://www.materialssquare.com/

Molecular dynamics simulation were performed using LAMMPS [1] package implemented in Materials Square [2].
[1] Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. Journal of computational physics, 117(1), 1-19.
[2] Virtual Lab. Inc., (2017, January 01). Materials Square. https://www.materialssquare.com/

Phase diagram was obtained by CALPHAD approach [1] implemented in Materials Square [2].
[1] Sundman, B., Kattner, U. R., Palumbo, M., & Fries, S. G. (2015). OpenCalphad-a free thermodynamic software. Integrating Materials and Manufacturing Innovation, 4(1), 1-15.
[2] Virtual Lab. Inc., (2017, January 01). Materials Square. https://www.materialssquare.com/




The list shows the publications which applied the calculation results obtained by the calculation package implemented in Materials Square.


  • Yoon, H., Song, H. J., Hyoung, J. S., Jung, S. W., Haryanto, A., Lee, C. W., & Kim, D. W. (2024). Facet-engineered ruthenium oxide on titanium oxide oxygen evolution electrocatalysts for proton-exchange membrane water electrolysis.Applied Catalysis B: Environment and Energy, 124382.
  • Jang, K., Song, H. J., Park, J. B., Jung, S. W., & Kim, D. W. (2024). Magnesium Fluoride-Engineered UiO-66 Artificial Protection Layers for Dendrite-Free Lithium Metal Batteries. Energy & Environmental Science.
  • Lee, D., Choi, C., Park, J. B., Jung, S. W., & Kim, D. W. (2024). Ingenious Separator Architecture: Revealing the Versatile 3D Heterostructured MXene-Hydrogen Titanate Electrocatalysts for Advanced Lithium-Sulfur Battery. Energy Storage Materials, 103529.
  • Kumar, K., de Leeuw, N., Adam, J., & Mishra, A. K. (2024). CO2 activation on pristine and Cu-decorated ψ-graphene and its hydrogenated forms: A DFT (D)+ U Study.
  • Kwon, S. Y., Lee, K., & Lee, J. H. (2024). Investigation into saturable absorption mechanism of bulk GeS particles at short-wavelength infrared band. Optical Materials, 149, 115005.
  • Yang, M., Shi, Z., He, Z., & Wang, D. (2024). Unraveling electrolyte solvation architectures for high-performance lithium-ion batteries. Science China Technological Sciences, 67(3), 958-964.
  • Jang, K., Yoon, H., Hyoung, J. S., Pratama, D. S. A., Lee, C. W., & Kim, D. W. (2024). Enhancement of hydrogen evolution activity by tailoring the electronic structure in ruthenium-heteroatom-doped cobalt iron phosphide nanoframes. Applied Catalysis B: Environmental, 341, 123327.
  • Lee, K., Kwon, S. Y., Choi, J., Kim, J., Woo, T., Ryu, J., ... & Lee, J. H. (2024). Third-order optical nonlinearities of Nb 4 C 3 MXene and its application as an ultra-broadband mode-locker. Journal of Materials Chemistry C, 12(3), 893-902.
  • Jung, K., Pratama, D. S. A., Haryanto, A., Jang, J. I., Kim, H. M., Kim, J. C., ... & Kim, D. W. (2024). Iridium-Cluster-Implanted Ruthenium Phosphide Electrocatalyst for Hydrogen Evolution Reaction. Advanced Fiber Materials, 6(1), 158-169.
  • Kim, H. J., Choi, J. H., Lee, S., Han, G. S., & Jung, H. S. (2024). Facet-Controlled Growth of Hydroxyapatite for Effectively Removing Pb from Aqueous Solutions. ACS Omega. 9(2), 2730-2739.
  • Park, J. B., Choi, C., Jung, S. W., Min, B. C., Park, J. H., & Kim, D. W. (2024). Designing Chemically Replaced Interfacial Layer via Unveiling the Influence of Zn Crystal Facets for Practical Zn‐Metal Anodes. Advanced Materials, 36(1), 2308684.
  • Lee, S. B., Park, C., Park, S. H., Lee, Y., & Yeo, J. S. Effect of Nitrogen Doping on Characteristics of Site Ovonic Threshold Switch for Selectors. Available at SSRN, 4681334.
  • Aldulaijan, S., Ajeebi, A. M., Jedidi, A., Messaoudi, S., Raouafi, N., & Dhouib, A. (2023). Surface modification of graphene with functionalized carbenes and their applications in the sensing of toxic gases: a DFT study. RSC advances, 13(28), 19607-19616.
  • Johnson, A., Ikyumbur, T. J., & Gbaorun, F. (2023). Optoelectronic Study of (MA) 2NaBiX6 (MA= methylammonium; X= Cl, Br, I) Hybrid Double Perovskites by Ab initio Simulation.arXiv preprint arXiv:, 2306.06417.
  • Bany Salman, M., Park, M., & Banisalman, M. J. (2023). Atomistic Study for the Tantalum and Tantalum–Tungsten Alloy Threshold Displacement Energy under Local Strain. International Journal of Molecular Sciences, 24(4), 3289.
  • im, S. M., Park, W. R., Park, J. S., Song, S. M., & Kwon, O. H. (2023). Effect of Defects in Graphene/Cu Composites on the Density of States. Materials, 16(3), 962.
  • Ramos, B. G., & Castriciones, E. V. (2023). Adhesion and bonding at the Ag (110)/Au (110) interface, a DFT study. Journal of Molecular Graphics and Modelling, 118, 108342.
  • Bang, J., Moon, I. K., Kim, Y. K., & Oh, J. (2023). Heterostructured Mo2N–Mo2C Nanoparticles Coupled with N‐Doped Carbonized Wood to Accelerate the Hydrogen Evolution Reaction. Small Structures, 2200283.
  • Lee, K., Han, H., Ryu, J. H., Kang, S., Jung, K., Kim, Y. K., ... & Kim, K. M. (2023). Laser-driven formation of ZnSnO3/CNT heterostructure and its critical role in boosting performance of the triboelectric nanogenerator. Carbon, 212, 118120.
  • Lim, G., Lee, J., Jung, J., & Lee, J. H. (2023). Highly stable Fabry-Pérot fiber-optic modulation device based on the photothermal effect of V2C MXene. Optics & Laser Technology, 157, 108671.
  • Kolivand, N., Haghighat-Shishavan, S., Nazarian-Samani, M., Kheradmandfard, M., Nazarian-Samani, M., Kashani-Bozorg, S. F., & Lee, W. (2023). Firmly Interlocked Janus-Type Metallic Ni3Sn2S2-Carbon Nanotube Heterostructure Suppresses Polysulfide Dissolution and Sn Aggregation. Journal of Colloid and Interface Science.
  • Mishra, P. K., Dash, A., Rini, E. G., Dobhal, R., Sengupta, A., & Sen, S. (2023). Defects altered n/p-type Fe/Ga modified ZnO for photo-sensing applications. Materials Today Communications, 106371.
  • Sengupta, A. (2022). First principles study of Li adsorption properties of a Borophene based hybrid 2D material B5Se. Applied Surface Science Advances, 8, 100218.
  • Johnson, A., Gbaorun, F., & Ikyo, B. A. (2022). First-principles study of (CsMA) NaSbX6 (MA= methylammonium; X= Cl, Br, I) organic–inorganic hybrid double perovskites for optoelectronic applications. Journal of Computational Electronics, 21(1), 34-39.
  • Lee, S., Kim, W. B., Kim, H. J., Choi, J. H., Lee, J. M., Gong, O. Y., & Jung, H. S. (2022). Combinatorial Physical Vapor Deposition: A New Methodology for Exploring Eco‐friendly Composition for Halide‐based Resistive Switching Memory. Advanced Materials Interfaces, 9(18), 2200662.
  • Kesek, M., & Kurt, K. (2022). First-principles calculations to investigate structural, electronic and phonon properties of sodium bromide (NaBr) and sodium iodide (NaI) crystals. Computational Condensed Matter, 31, e00682.
  • Bang, J., Moon, I. K., Choi, K., & Oh, J. (2022). Phase-engineering terraced structure of edge-rich α-Mo2C for efficient hydrogen evolution reaction. Materials Today Energy, 100981.
  • Ouserigha, C. E., & Benjamin, A. K. Density Functional Theory Study on the Electronic Properties of Mg Doped FePS3.
  • Park, B. C., Ko, M. J., Kim, Y. K., Kim, G. W., Kim, M. S., Koo, T. M., ... & Kim, Y. K. (2022). Surface-ligand-induced crystallographic disorder–order transition in oriented attachment for the tuneable assembly of mesocrystals. Nature Communications, 13(1), 1-11.
  • Sengupta, A. (2022). First principles design of 2 dimensional Nickel dichalcogenide Janus materials NiXY (X, Y= S, Se, Te). Computational Materials Science, 206, 111278.
  • Sengupta, A. (2022). First principles study of Li adsorption properties of a Borophene based hybrid 2D material B5Se. Applied Surface Science Advances, 8, 100218.
  • Mishra, P. K., Viji, P., Dobhal, R., Sengupta, A., Rini, E. G., & Sen, S. (2022). Defects assisted photosensing and dye degradation of Ni/Ga co-doped ZnO: A theory added experimental investigation. Journal of Alloys and Compounds, 893, 162229.
  • Lee, J., Kwon, S. Y., & Lee, J. H. (2022). Harmonically mode-locked Er-doped fiber laser at 1.3 GHz using a V2AlC MAX phase nanoparticle-based saturable absorber. Optics & Laser Technology, 145, 107525.
  • Lee, G. W., Choi, Y. J., Kim, Y. H., Park, B. H., Choi, S. G., Nazarian-Samani, M., & Kim, K. B. (2022). Amorphization of germanium selenide driven by chemical interaction with carbon and realization of reversible conversion-alloying reaction for superior K-ion storage. Chemical Engineering Journal, 430, 132995.
  • Enkhtuvshin, E., Kim, K. M., Kim, Y. K., Mihn, S., Kim, S. J., Jung, S. Y., ... & Han, H. (2021). Stabilizing oxygen intermediates on redox-flexible active sites in multimetallic Ni–Fe–Al–Co layered double hydroxide anodes for excellent alkaline and seawater electrolysis. Journal of Materials Chemistry A.
  • Lee, J., Lee, K., & Lee, J. H. (2021). Nonlinear absorption property investigation into MAX phase Ti 2 AlC at 1.9 μm. Optical Materials Express, 11(10), 3556-3566.
  • Lee, J., Kwon, S. Y., & Lee, J. H. (2021). Investigation on the nonlinear optical properties of V 2 C MXene at 1.9 μm. Journal of Materials Chemistry C, 9(42), 15346-15353.
  • Lee, S., Kim, W. B., Lee, J. M., Kim, H. J., Choi, J. H., & Jung, H. S. (2021). Oxide Passivation of Halide Perovskite Resistive Memory Device: A Strategy for Overcoming Endurance Problem. ACS Applied Materials & Interfaces, 13(37), 44577-44584.
  • Johnson, A., Gbaorun, F., & Ikyo, B. A. (2021). First-Principles Study of (CsMA) NaSbX6 (MA= Methylammonium; X= Cl, Br, I) Organic-Inorganic Hybrid Double Perovskites For Optoelectronic Applications.
  • Sengupta, A. (2021). Lithium adsorption properties of monolayer B5Se. arXiv preprint arXiv:2101.08462.
  • Sengupta, A. (2021). An ab-initio study of 2 dimensional metal (Cu, Ag)-1T’ReS 2 van der Waals heterostructure. 2021 Devices for Integrated Circuit (DevIC), 221-223.
  • Sengupta, A. (2021). First principles design of 2 dimensional Nickel dichalcogenide Janus materials NiXY. arXiv preprint arXiv:2110.08593.
  • Kwon, S. Y., Lee, J., & Lee, J. H. (2021). Passive mode-locking by a Ti2AlN saturable absorber in 1.5 μm region. Optik, 168364.
  • Choi, Y. J., Lee, G. W., Kim, Y. H., Kim, H. K., & Kim, K. B. (2021). Graphene with Nanoperforation for High-Capacity Potassium-Ion Storage: Decoupling Structural Defect and Doping Effects of N-doped Graphene. Chemical Engineering Journal, 134260.
  • Esfandiari, A., Haghighat-Shishavan, S., Nazarian-Samani, M., Nazarian-Samani, M., Ramakrishna, S., Kashani-Bozorg, S. F., & Kim, K. B. (2020). Defect-rich Ni3Sn4 quantum dots anchored on graphene sheets exhibiting unexpected reversible conversion reactions with exceptional lithium and sodium storage performance. Applied Surface Science, 526, 146756.
  • Haghighat-Shishavan, S., Nazarian-Samani, M., Nazarian-Samani, M., Roh, H. K., Chung, K. Y., Oh, S. H., ... & Kim, K. B. (2019). Exceptionally reversible Li-/Na-ion storage and ultrastable solid-electrolyte interphase in layered GeP5 anode. ACS applied materials & interfaces, 11(36), 32815-32825.


  • Chahal, R., Toomey, M. D., Kearney, L. T., Sedova, A., Damron, J. T., Naskar, A. K., & Roy, S. (2024). Deep-Learning Interatomic Potential Connects Molecular Structural Ordering to the Macroscale Properties of Polyacrylonitrile. ACS Applied Materials & Interfaces.
  • Alnairi, M. M., & Jaser Banisalman, M. (2024). Molecular Dynamics Analysis of Collison Cascade in Graphite: Insights from Multiple Irradiation Scenarios at Low Temperature. Crystals, 14(6), 522.
  • Bany Salman, M., Park, M., & Banisalman, M. J. (2023). Atomistic Study for the Tantalum and Tantalum–Tungsten Alloy Threshold Displacement Energy under Local Strain. International Journal of Molecular Sciences, 24(4), 3289.
  • Bany Salman, M., Park, M., & Banisalman, M. J. (2022). A Molecular Dynamics Study of Tungsten’s Interstitial Dislocation Loops Formation Induced by Irradiation under Local Strain. Solids, 3(2), 219-230.
  • Salman, M. B., Park, M., & Banisalman, M. J. Atomistic Investigation of Interstitial Dislocation Loop Formation in Tantalum and Tantalum-Tungsten Alloy under by Low Temperature Irradiation under Local Deformation.
  • Salman, M. B., Park, M., & Banisalman, M. J. (2023). Revealing the Effects of Strain and Alloying on Primary Irradiation Defects Evolution in Tantalum Through Atomistic Simulations. Metals and Materials International, 1-12.
  • Kilic, M. E., Lee, J. H., & Lee, K. R. (2021). Oxygen ion transport in doped ceria: effect of vacancy trapping. Journal of Materials Chemistry A.


  • Awais, M. (2023). Microstructure Evolution and Deformation Micromechanisms of Nickel and Refractory Superalloys (Doctoral dissertation, University of Miami).
  • Awais, M., Hixson, W. R., Victor, Q., O’Neal, C., Ilavsky, J., & Coakley, J. (2023). Microstructure Evolution of a Multimodal Gamma-Prime Ni-Based Superalloy Characterized by In Situ Diffraction. Metallurgical and Materials Transactions A, 54(6), 2311-2319.


This page has been created by SimPL. Last update:Feb 04, 2022 / © Copyright 2018-2022 Virtual Lab. Inc.